Teoria das categorias

Na matemática, a teoria das categorias provê uma linguagem interdisciplinar capaz de delinear resultados e construções gerais, separando-os dos específicos a cada área, possibilitando a simplificação e clarificação de demonstrações. A teoria centra-se nos conceitos de categoria, que é uma abstração do conceito de composição de funções, de functor, transformações entre categorias, e de transformação natural, a qual provê um significado preciso para expressões como "natural" e "canônico".^[1]

O conceito de categorias, functores e transformações naturais, em maior generalidade, foi introduzido por Samuel Eilenberg e Saunders Mac Lane, em 1945, em seu artigo "General Theory of Natural Equivalences". Nos anos seguintes, a teoria das categorias foi empregada na topologia algébrica e álgebra homológica, por Norman Steenrod, Alexander Grothendieck e outros. Em 1958, Daniel Kan descobre o conceito de functores adjuntos, que, segundo Mac Lane, são "onipresentes na matemática".^[2]^[3]^[4]^[5] Desde então, houve diversos desenvolvimentos.^[6]

Sendo de alto nível de abstração, é recomendada, antes do estudo de teoria das categorias, familiaridade de conceitos básicos de álgebra linear, álgebra abstrata e topologia, por exemplo.^[1]

Categoria

Uma categoria $C$ consiste nos seguintes elementos:

Uma coleção de objetos de $C$ .
Para cada dupla $a, b$ de objetos, uma coleção de setas (ou morfismos) do domínio (ou origem) $a$ até o contradomínio (ou destino) $b$ , para as quais são usadas a notações $f : a \to b$ e $f \in hom C (a, b)$ .
Para cada objeto $a$ , uma seta de $a$ até $a$ , chamada identidade $1 a : a \to a$ .
Para cada tripla de objetos $a, b, c$ , uma operação de composição, levando
cada seta $f : a \to b$ e cada seta $g : b \to c$ a uma seta $g \circ f : a \to c$ .
Devem ser satisfeitas as igualdades:
(Lei da identidade) Para todos objetos $a, b$ e todas as setas $f : a \to b$ , vale $1 b \circ f = f = f \circ 1 a$ .
(Associatividade) Para todos objetos $a, b, c, d$ e todas as setas $f : a \to b$ , $g : b \to c$ e $h : c \to d$ , vale $(h \circ g) \circ f = h \circ (g \circ f)$ .^[7]^[8]^[9]

Há, por exemplo, categorias:

cujos objetos são conjuntos, e cujos morfismos são funções entre conjuntos;
cujos objetos são grupos, e cujos morfismos são homomorfismos de grupos;
cujos objetos são espaços topológicos, e cujos morfismos são funções contínuas;
cujos objetos são os elementos de um conjunto pré-ordenado fixo $(P, \leq)$ , e tal que, para quaisquer objetos $x, y \in P$ , o número de morfismos $x \to y$ é exatamente um se $x \leq y$ , e zero se $\neg (x \leq y)$ .^[10]
cujos objetos são vértices de um grafo, e cujos morfismos são caminhos nesse grafo.^[11]

Nestes dois últimos exemplos, percebe-se que os objetos podem não ter "elementos", e os morfismos podem não ter relação com funções.

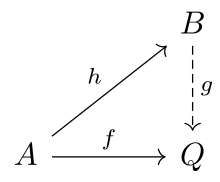
O diagrama acima é comutativo exatamente quando

f = g \circ h

.

Para a representação de relações entre os morfismos, usam-se diagramas consistindo de alguns dos objetos e setas de uma categoria; uma sequência de setas, cada uma tendo destino coincidindo com a origem da seguinte, representa a composição de morfismos correspondentes. Um desses diagramas é chamado diagrama comutativo quando quaisquer duas sequências de setas que iniciam num mesmo objeto, e que terminam também num mesmo objeto, têm composições iguais.^[12]^[13]

Dualizar consiste em inverter o sentido de cada uma das setas em um diagrama; cada categoria tem uma categoria oposta. Desse modo, os teoremas e definições em teoria das categorias se organizam em duplas, um enunciado sendo obtido do outro trocando cada categoria pela oposta; por exemplo, um epimorfismo é um monomorfismo na categoria oposta, um coproduto é um produto na categoria oposta etc.^[14]

Tipos de morfismos

Como os objetos de uma categoria podem não ter "elementos", generalizações de conceitos como função injetiva e função sobrejetiva devem envolver somente setas, e pode haver mais de uma generalização possível.

	Como uma categoria consiste de setas, nossa disciplina também poderia ser descrita como aprender como viver sem elementos, usando setas em vez deles.
— Saunders Mac Lane^[15]

Como exemplo, generalizando o conceito de função injetiva, um morfismo $f : a \to b$ é chamado monomorfismo se e só se

para todo objeto

c

e morfismos

g, h : c \to a

satisfazendo

f \circ g = f \circ h

, vale

g = h

.

Na categoria dos conjuntos, na categoria dos grupos e na categoria dos espaços topológicos, os monomorfismos são exatamente as funções injetivas.^[16] Já um morfismo $f : a \to b$ é chamado seção se e só se existe $g : b \to a$ tal que $g \circ f = 1 a$ . Toda seção é um monomorfismo, mas a recíproca pode falhar; com efeito, na categoria dos grupos abelianos, as seções são exatamente os homomorfismos de grupos abelianos $f : A \to B$ que são injetivos e tais que $B$ é a soma direta da imagem de $f$ com algum subgrupo de $B$ .^[17]

Dualizando, um morfismo $f : b \to a$ é um epimorfismo se e só se

para todo objeto

c

e morfismos

g, h : a \to c

satisfazendo

g \circ f = h \circ f

, vale

g = h

.

Na categoria dos conjuntos, os epimorfismos são precisamente as funções sobrejetivas. Na categoria dos anéis, no entanto, a inclusão $ℤ \to ℚ$ é um epimorfismo não sobrejetivo.^[18]

Como outro exemplo, um isomorfismo é um morfismo $f : a \to b$ tal que há $g : b \to a$ satisfazendo $g \circ f = 1 a$ e $f \circ g = 1 b$ . Na categoria dos espaços topológicos, os isomorfismos são precisamente os homeomorfismos.^[19]

Propriedade universal

Construções como produto cartesiano, soma direta, e espaço funcional podem ser generalizadas para todas as categorias. Com exemplo, dados objetos $a, b$ numa categoria $C$ , um objeto $a \times b$ , junto a morfismos $p a : a \times b \to a$ e $p b : a \times b \to b$ , forma um sistema de produto categorial (binário) se e só se, para qualquer outro objeto $c$ e quaisquer morfismos $f : c \to a$ e $g : c \to b$ , existe único morfismo $h : c \to a \times b$ tal que $p a \circ h = f$ e $p b \circ h = g$ .

Diagrama representado o produto categorial.

Dualmente, há o conceito de coproduto (binário). Na categoria dos conjuntos, os produtos correspondem aos produtos cartesianos, e os coprodutos correspondem às uniões disjuntas. Na categoria dos grupos abelianos, os produtos e coprodutos binários coincidem, e são chamados de soma direta.^[20]^[21]

Uma propriedade universal é uma propriedade que envolve a existência de único morfismo que faz certo diagrama comutar. Maneiras de definir rigorosamente o conceito incluem functores representáveis e limites e colimites.^[22]^[23]

Functor

	[…] sempre que novos objetos abstratos são construídos de uma maneira especificada a partir de outros, é recomendado tratar a construção dos mapeamentos induzidos correspondentes nesses novos objetos como parte integral de sua definição.
— Samuel Eilenberg, Saunders Mac Lane^[24]

Um functor é uma correspondência entre objetos de duas categorias que pode ser estendida a uma correspondência entre morfismos, de modo que sejam preservadas as identidades e as composições. Mais precisamente, dadas categorias $C$ e $D$ , um functor (covariante) de $C$ até $D$ , escrito $F : C \to D$ , consiste

de uma atribuição, a cada objeto $x \in C$ , de um objeto $F (x) \in D$ ,
de uma atribuição, a cada morfismo $f : x \to y$ , de um morfismo $F x, y (f) = F (f) : F (x) \to F (y)$ ,

satisfazendo

$F (1 x) = 1 F (x)$ para cada objeto $x \in C$ ,
$F (g \circ f) = F (g) \circ F (f)$ para cada dupla de morfismos $f : x \to y$ e $g : y \to z$ .

Exemplos de correspondências que podem ser estendidas a functores são: a correspondência entre cada conjunto $A$ e seu conjunto de partes $P(A)$ (levando cada $f : A \to B$ à função $f \to = (S \subseteq A) \mapsto {f (x) | x \in S}$ , de imagens de subconjuntos de $A$ ); a correspondência entre cada anel comutativo $K$ e seu grupo de matrizes invertíveis $GL n (K)$ de ordem $n$ .^[25]

Noutros casos, há um functor contravariante, atribuindo um morfismo $F (f) : F (y) \to F (x)$ a cada morfismo $f : x \to y$ , e invertendo a ordem das composições. Exemplos de correspondências que podem ser estendidas a functores contravariantes são: a correspondência entre cada conjunto e seu conjunto de partes (levando cada $f : A \to B$ à função $f \leftarrow = (T \subseteq B) \mapsto {y | f (y) \in T}$ , de pré-imagens de subconjuntos de $B$ ); a correspondência entre cada espaço vetorial e seu espaço dual; a correspondência entre cada anel comutativo e seu espaço de ideais primos.^[26]

Transformação natural

	Não é muito enganoso, pelo menos historicamente, dizer que categorias são o que deve ser definido para definir functores, e que functores são o que deve ser definido para definir transformações naturais.
— Peter Freyd^[27]

Intuitivamente, uma transformação natural é uma família de morfismos numa categoria dados simultaneamente por uma mesma definição, sem depender de escolhas "arbitrárias". Por exemplo, para cada $V$ espaço vetorial, há mapeamento linear natural $e$ de $V$ ao dual de seu dual, dado por $e (v) = f \mapsto f (v)$ . Mais precisamente, uma transformação natural entre functores $F, G : C \to D$ é uma família de morfismos $η X : F (X) \to G (X)$ , para cada $X$ objeto de $C$ , satisfazendo

para qualquer morfismo

f : X \to Y

,

η Y \circ F (f) = G (f) \circ η X

.^[28]

Diagrama comutativo da condição de naturalidade.

Eis exemplos:

A projeção $G \to G ∕[G, G]$ de cada grupo em sua abelianização (quociente pelo subgrupo comutador) pode ser representada como uma transformação natural.^[29]
A dualidade de Pontryagin pode ser descrita como a existência de isomorfismo natural $G ≅ G \land\land$ , para cada $G$ grupo abeliano localmente compacto, onde $H \land$ denota o grupo topológico dos homomorfismos contínuos de $H$ a $𝕋$ , grupo multiplicativo dos complexos de valor absoluto um.^[30]

Functores e transformações naturais permitem definir o conceito de equivalência de categorias.

Adjunção

Uma adjunção entre functores $F : C \to D$ e $G : D \to C$ é uma família natural de isomorfismos, para quaisquer objetos $c$ de $C$ e $d$ de $D$ ,

\hom _{D}(F(c),d)\cong \hom _{C}(c,G(d)).

Neste caso, diz-se que

F

é adjunto esquerdo e

G

é adjunto direito. Exemplos de adjunções incluem:

Sendo $C = Set$ a categoria de conjuntos e $D = K - Vet$ a categoria de espaços vetoriais sobre um corpo fixo $K$ , a adjunção $\hom _{K-\mathbf {Vet} }(K[S],V)\cong \hom _{\mathbf {Set} }(S,G(V))$ onde $K [S]$ é um espaço vetorial de base indexada pelo conjunto $S$ , e $G (V)$ é o conjunto de elementos do espaço vetorial $V$ .^[31]
Sendo $C = Set$ a categoria de conjuntos e $D = Grp$ a categoria de grupos, a adjunção $\hom _{\mathbf {Grp} }(F(S),H)\cong \hom _{\mathbf {Set} }(S,G(H))$ onde $F (S)$ é o grupo livre no conjunto $S$ , e $G (H)$ é o conjunto de elementos do grupo $H$ .
Sendo $D = CompMet$ a categoria dos espaços métricos completos (cujos morfismos são os mapeamentos uniformemente contínuos) e $C = Met$ a categoria dos espaços métricos, a adjunção $\hom _{\mathbf {CompMet} }(K(M),N)\cong \hom _{\mathbf {Met} }(M,G(N))$ onde $K (M)$ é a completação do espaço métrico $M$ , e $G (N) = N$ .^[32]
Sendo $C = D = Ab$ a categoria dos grupos abelianos, e sendo $H$ grupo abeliano fixo, a adjunção $\hom _{\mathbf {Ab} }(A\otimes H,B)\cong \hom _{\mathbf {Ab} }(A,\operatorname {Hom} (H,B))$ onde $\otimes$ denota o produto tensorial entre grupos abelianos, e $Hom(H, B)$ denota o grupo abeliano de homomorfismos de grupo $H \to B$ .^[33]
Sendo $C = Top$ a categoria dos espaços topológicos e $D = CHaus$ a categoria dos espaços compactos de Hausdorff, a adjunção $\hom _{\mathbf {CHaus} }(F(X),K)\cong \hom _{\mathbf {Top} }(X,G(K))$ onde $F (X)$ é a compactificação de Stone–Čech de $X$ , e $G (K) = K$ .^[34]

Se um functor $F : C \to D$ é adjunto esquerdo a $G : D \to C$ , a composição $G \circ F : C \to C$ faz parte de uma mônade em $C$ .^[35]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

Pesquisar este blog

MATEMÁTICA GRACELI DIMENSIONAL

Teoria das categorias

Índice

Categoria

Tipos de morfismos

Propriedade universal

Functor

Transformação natural

Adjunção

Comentários

Postar um comentário

Postagens mais visitadas deste blog